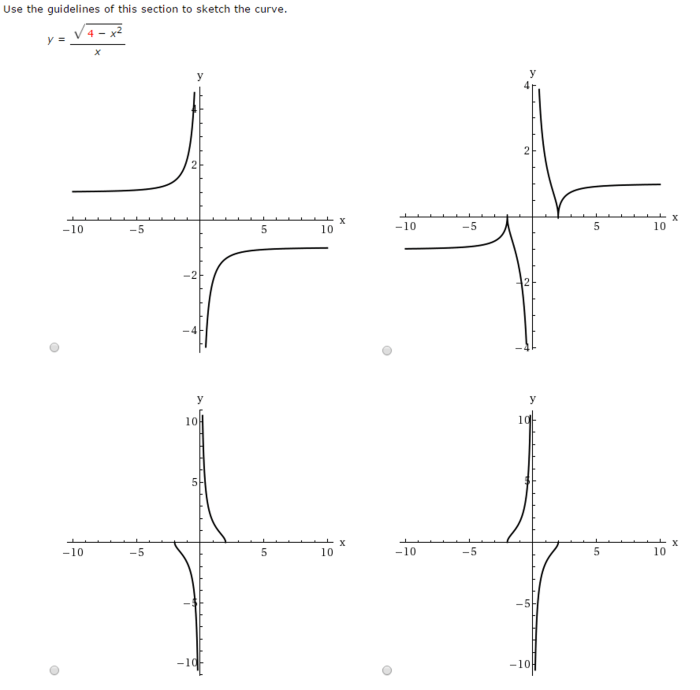
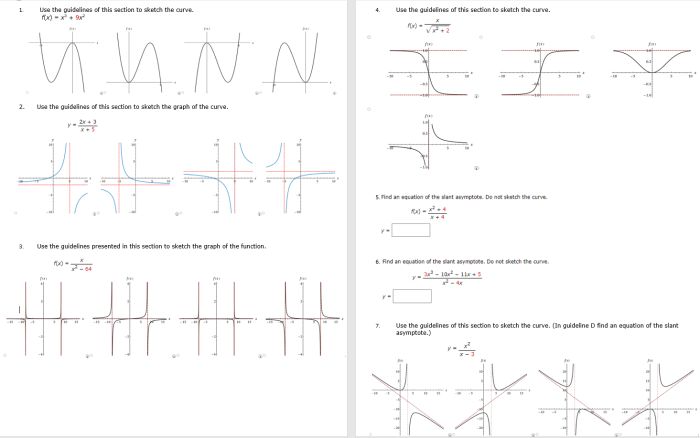
Use the guidelines of this section to sketch the curve. – Embark on an enlightening journey into the realm of curve sketching, where we delve into the essential guidelines that empower you to unravel the intricate world of curves. This comprehensive guide unveils the purpose, principles, and techniques that will transform you into a proficient curve sketching maestro.
As we navigate through this exploration, we will uncover the practical applications of curve sketching, ranging from data analysis to problem-solving. Real-world examples will illuminate the profound impact of curve sketching in diverse fields, showcasing its invaluable role in shaping our understanding of complex phenomena.
Understanding the Guidelines

The guidelines provided in this section offer a comprehensive framework for sketching curves effectively and accurately. They establish key principles, techniques, and considerations to ensure that the resulting curves accurately represent the underlying data or functions.
Sketching the Curve

To sketch a curve based on the guidelines, follow these steps:
- Identify the key features of the curve, such as intercepts, extrema, and points of inflection.
- Determine the slope and curvature of the curve at various points.
- Use the guidelines to determine the shape and behavior of the curve.
- Sketch the curve using appropriate techniques, such as freehand drawing or computer-aided design.
Applications of Curve Sketching: Use The Guidelines Of This Section To Sketch The Curve.
Curve sketching finds practical applications in various fields:
- Data analysis: Visualizing trends, patterns, and relationships in data.
- Problem-solving: Analyzing complex systems, optimizing solutions, and making predictions.
- Engineering: Designing structures, analyzing forces, and predicting performance.
- Economics: Modeling economic behavior, forecasting trends, and evaluating policies.
Advanced Techniques
For complex curves, advanced techniques may be necessary:
- Approximating curves using mathematical equations: Polynomials, exponential functions, or trigonometric functions.
- Using computer software: Specialized software for curve sketching and analysis, such as MATLAB or Mathematica.
- Employing numerical methods: Approximating derivatives and integrals to determine curve properties.
Examples and Demonstrations
Consider the function f(x) = x^2- 4x + 3 :
- Intercepts: (3, 0) and (1, 0)
- Vertex: (2, -1)
- Slope at x = 0: -4
- Curvature: Positive for x < 2, negative for x > 2
Using these properties, we can sketch the curve as a parabola that opens upward, with a minimum at (2, -1).
Query Resolution
What is the significance of the guidelines provided in this guide?
The guidelines Artikeld in this guide serve as a foundational framework for understanding the principles and techniques of curve sketching. They provide a structured approach to ensure accuracy and efficiency in your sketching endeavors.
How can I apply curve sketching to real-world problems?
Curve sketching finds widespread application in various fields, including physics, engineering, and economics. By analyzing the shape and characteristics of curves, you can gain valuable insights into the behavior of systems, solve complex problems, and make informed predictions.
What advanced techniques can I explore to enhance my curve sketching skills?
To refine your curve sketching abilities, consider exploring advanced techniques such as approximating curves using mathematical equations and leveraging computer software for automated sketching and analysis. These techniques will empower you to tackle more intricate curves and derive precise results.

