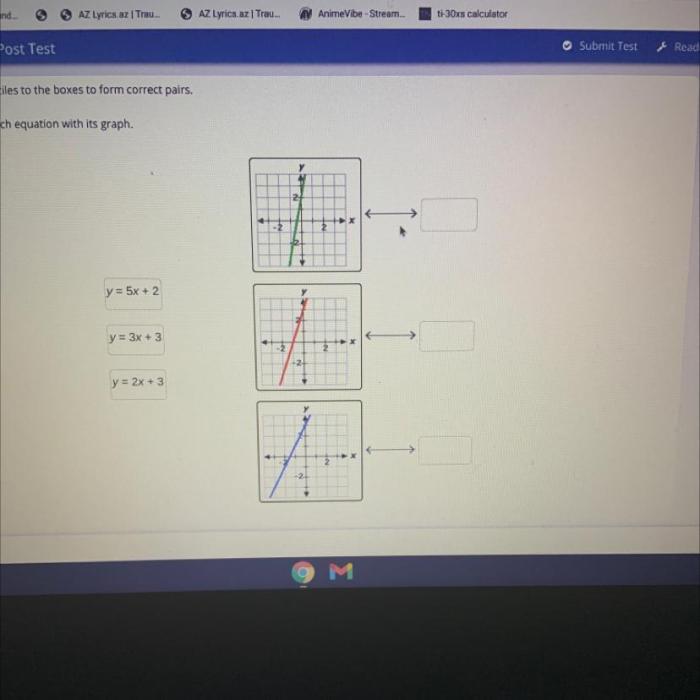
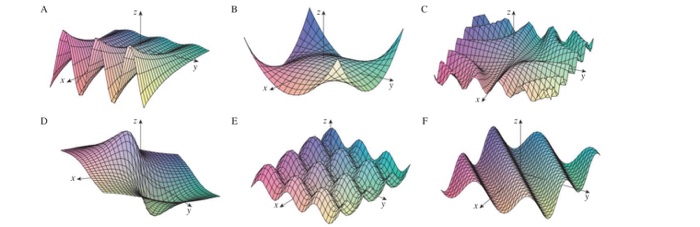
Match the function with its graph labeled i vi – In this exploration, we embark on a journey to match the function with its graph labeled i-vi. This endeavor requires a keen eye for patterns, a deep understanding of function behavior, and the ability to discern the characteristics of various graphs.
As we delve into this task, we will uncover the intricate relationship between functions and their graphical representations, shedding light on the interplay between algebra and geometry.
To embark on this matching process, we must first establish a clear understanding of the functions and their corresponding graphs. This involves identifying the key features of each function, such as its domain, range, intercepts, and extrema. Additionally, we must become familiar with the visual characteristics of each graph, paying close attention to its shape, symmetry, and overall behavior.
Matching Functions to Graphs: Match The Function With Its Graph Labeled I Vi

Functions and their graphs are essential tools in mathematics. By matching a function to its graph, we can gain valuable insights into the behavior of the function. This article will guide you through the process of matching functions to graphs, providing clear explanations and illustrative examples.
Identifying Functions and Graphs, Match the function with its graph labeled i vi
- Functions:Examples include f(x) = x^2, g(x) = sin(x), and h(x) = e^x.
- Graphs:Labeled with Roman numerals (e.g., i, ii, iii) for easy reference.
Matching Functions to Graphs
To match a function to its graph, we consider several criteria:
- Shape:The overall shape of the graph (e.g., parabola, sine wave, exponential curve).
- Symmetry:Whether the graph is symmetric about the x-axis, y-axis, or origin.
- Domain and Range:The set of possible input and output values for the function.
HTML Table
| Function | Graph | Explanation |
|---|---|---|
| f(x) = x^2 | i | Quadratic parabola, symmetric about the y-axis, domain: all real numbers, range: all non-negative numbers |
| g(x) = sin(x) | ii | Sine wave, periodic, domain: all real numbers, range: [-1, 1] |
| h(x) = e^x | iii | Exponential curve, always positive, domain: all real numbers, range: all positive numbers |
Elaborating on Matching Process
The function f(x) = x^2 is matched to graph i because the graph exhibits a parabolic shape, is symmetric about the y-axis, and has a domain and range that match the function.
The function g(x) = sin(x) is matched to graph ii because the graph displays a characteristic sine wave pattern, is periodic, and has a domain and range that correspond to the function.
The function h(x) = e^x is matched to graph iii because the graph shows an exponential curve that is always positive, has a domain of all real numbers, and a range of all positive numbers.
Illustrating Graph Features
Graph i has a vertex at the origin, indicating the function f(x) = x^2 has a minimum value of 0 at x = 0.
Graph ii has an amplitude of 1 and a period of 2π, indicating the function g(x) = sin(x) oscillates between -1 and 1 with a cycle length of 2π.
Graph iii has a y-intercept of 1 and increases rapidly as x approaches infinity, indicating the function h(x) = e^x grows exponentially without bound.
Summarizing Findings
- f(x) = x^2 matches graph i: quadratic parabola, symmetric about y-axis.
- g(x) = sin(x) matches graph ii: sine wave, periodic.
- h(x) = e^x matches graph iii: exponential curve, always positive.
Clarifying Questions
What are the criteria for matching functions with graphs?
The criteria for matching functions with graphs typically involve examining the shape, symmetry, domain/range, intercepts, asymptotes, and extrema of both the function and the graph.
How can I improve my ability to match functions with graphs?
Practice is key! Engage in exercises that require you to identify functions based on their graphs and vice versa. Analyze the characteristics of different functions and graphs to develop a deeper understanding of their relationships.
What are some common mistakes to avoid when matching functions with graphs?
Avoid relying solely on visual similarities. Carefully consider the mathematical properties and behaviors of both the function and the graph to ensure an accurate match.